Visualization Lab
1. Molecular Orbitals
Understanding Organic Reactivity
What are some of the fundamental principles that govern the reactivity of molecules? What makes a molecule a good nucleophile or a strong electrophile? How can we predict which position of an aromatic ring undergoes electrophilic or nucleophilic substitutions? The simple understanding that a nucleophile is an electron-rich molecule that attacks sites with low electron density, and that electrophiles are electron-poor molecules that will attack a position of large electron density allows an understanding of many organic reactions.
In other situations, this simple understanding is insufficient. For example, how can we rationalize the observed preference for nitration of the 1-position in naphthalene by nitric acid if the total π electron densities in the 1 and 2 position are expected to be the same? In principle, the answer can be reached by considering the structures and energies of the two transition states leading to the two products, but this approach is often impractical.

Frontier Orbital Theory
 A powerful practical model for describing
chemical reactivity is the frontier molecular orbital (FMO) theory, developed
by Kenichi Fukui in the 1950's. An important aspect of the FMO theory is the
focus on the highest occupied and lowest unoccupied molecular orbitals (HOMO
and LUMO). For example, instead of thinking about the total electron density in
a nucleophile, we should think about the localization of HOMO orbital.
Electrons from this orbital are the most available to participate in a
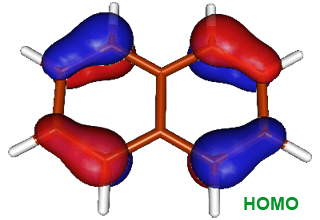
reaction. The image on the right shows the HOMO of naphthalene; we can see that
the frontier electron density is highest at position 1.
A powerful practical model for describing
chemical reactivity is the frontier molecular orbital (FMO) theory, developed
by Kenichi Fukui in the 1950's. An important aspect of the FMO theory is the
focus on the highest occupied and lowest unoccupied molecular orbitals (HOMO
and LUMO). For example, instead of thinking about the total electron density in
a nucleophile, we should think about the localization of HOMO orbital.
Electrons from this orbital are the most available to participate in a
reaction. The image on the right shows the HOMO of naphthalene; we can see that
the frontier electron density is highest at position 1.
Similarly, the FMO theory predicts that a site where the lowest occupied orbital is localized, is a good electrophilic site. The FMO theory was initially used for explaining the electrophilic substitution in naphthalene but it became gradually clear that the scope of this theory is much broader. For example, the concept of frontier orbital symmetries was successfully used to rationalize the outcomes of cycloaddition reactions and other pericyclic reactions.
Calculating and Visualizing Molecular Orbitals
Standard quantum chemistry calculations yield delocalized molecular orbital. In Gaussian, the keyword Pop requests printout of molecular orbitals. Alternatively, keywords GFINPUT, IOP(6/7)=3 can be used to greate output that can be visualized with JMOL and MOLDEN. You can download the Gaussian-03 input file and output file that contains a geometry optimzed structure and MO information for naphthalene. You do not need to repeat this calculation because it will be time consuming. Also notice that this calculation included some tretament of electron correlation by invoking the MP2 keyword; the result of this is that many MO orbitals will have fractional populations. You should inspect the input file to make sure that you understand the use of all the keywords.
· Download the latest
version of JMOL.
· Open the output file
(napthalene_mp2.log) with JMOL. The executable file for JMOL is
"jmol.jar."
· The Gaussian output
file contains all the intermediate structures from the geometry
optimization. These are all available in JMOL for display. To
select the lowest enegy (optimized) structure click on the JMOL icon in the
lower right side of the JMOL window. Select MAIN
MENU option, then MODEL 1/8 option
(the current structure displayed is the Gaussian input structure), and finally
choose the final structure in the list - this is the optimized geometry.
· You are now ready to
display the MOs as isocontour surfaces around the molecule. There are two ways
to do this:
1.In the MAIN MENU (from JMOL icon) select SURFACES, then MOLECULAR ORBITALS. You will then see another window with numbers
(in groups of 25) on it. These are the molecular orbitals, the are numbered
from the lowest energy orbital to the highest (the energies of these orbitals
in Hartrees are also listed). Select the first orbital. You should see MOs
centered at atoms: these are the core orbitals at heavy atoms that are not
involved in bonding. Inspect some other
2.In the FILE pulldown menu select SCRIPT. The JMOL Script Console will
open. This provides a very powerful way to interact with JMOL. In the
script console window type the command mo 1 and hit return. You
should see the first molecular orbital appear. You can change the look by
typing mo fill nomesh followed by
return. This should make the mo look solid rather than a mesh. Now
type mo translucent followed by
return. What happens now? There are many things you can do. Documentation for this
interactive scripting language is available from St. Olaf College. From the documentation menu open the "mo" link for command usage and examples.
· Using either method,
select the highest energy occupied MO (the least negative energy). This is one
of the bonding Pi orbitals.
· Compare your result
with the image in the tutorial.
· Play around some
more.
Molecular Orbitals in Conjugated Systems
 According to the frontier
orbital theory, the chemistry of conjugated π systems is largely determined by
the HOMO and LUMO π orbitals in the reactant molecules. The outcome of
reactions involving interaction of π orbitals can be rationalized using the
concepts of orbital phase and symmetry. The figure on the right illustrates
what is meant by the orbital phase using 1,3-butadiene as an example. In this
molecule, four atomic p orbitals form four π molecular orbitals. The four
molecular orbitals differ by the extent of favorable overlap, and thus in
energy. The lowest energy MO forms from the in-phase overlap of all four p atomic
orbitals; the next one forms when two pairs or in-phase atomic orbitals
overlap; the third when one pair of in-phase atomic orbitals overlaps, and the
highest energy molecular orbital forms when there are no in-phase overlaps. The
MO's are filled with electrons starting with the lowest-energy orbital such
that two electrons occupy an MO. In case of 1,3-butadiene, there are 4 π
electrons, thus the second lowest-energy orbital is the HOMO.
According to the frontier
orbital theory, the chemistry of conjugated π systems is largely determined by
the HOMO and LUMO π orbitals in the reactant molecules. The outcome of
reactions involving interaction of π orbitals can be rationalized using the
concepts of orbital phase and symmetry. The figure on the right illustrates
what is meant by the orbital phase using 1,3-butadiene as an example. In this
molecule, four atomic p orbitals form four π molecular orbitals. The four
molecular orbitals differ by the extent of favorable overlap, and thus in
energy. The lowest energy MO forms from the in-phase overlap of all four p atomic
orbitals; the next one forms when two pairs or in-phase atomic orbitals
overlap; the third when one pair of in-phase atomic orbitals overlaps, and the
highest energy molecular orbital forms when there are no in-phase overlaps. The
MO's are filled with electrons starting with the lowest-energy orbital such
that two electrons occupy an MO. In case of 1,3-butadiene, there are 4 π
electrons, thus the second lowest-energy orbital is the HOMO.
The Diels-Alder Reaction
The Diels-Alder reaction is a cycloaddition reaction between a conjugated diene and dienophile.
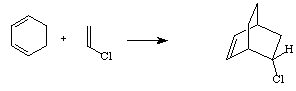

Diels-Alder reaction has high synthetic utility for making unsaturated six-membered rings. The reaction with unsubstituted dienophile (as shown above) is very slow but the Diels-Alder reactions occur readily when the alkene has a electron-withdrawing substituent. For example, acrolein is a good dienophile. Cycloalkenes, especially ones where the double bond is conjugated to a carbonyl, can be used as dienophiles. The diene is required to have an s-cis conformation and cyclic dienes work well in this reaction. For example, a reaction between 1,3-cyclohexadiene and chloroethene yields a bicyclic reaction product.
Note that chlorine is a relatively poor π-electron withdrawing group and the reaction above in not very fast. Interestingly, many Diels-Alder reactions occur much faster in water than in organic solvents. Scientists are still working on finding out why aqueous environment accelerates this reaction.
Molecular Orbitals in Diels-Alder Reaction
The Diels-Alder reaction is highly stereoselectivive: cis-substituted dienophiles yield cis-substituted cyclohexenes and trans-substituted dienophiles yield trans-substituted cyclohexenes. Stereoselectivity in Diels-Alder reaction can be rationalized considering the overlap of HOMO of one reactant with LUMO of the other.
· Using GridChem and
Gaussian calculate the MOs for ethylene and 1,3 butadiene. You can obtain
initial structures from Chem3D or any other program to construct molecules that
you are comfortable with. Minimize the geometry with some simple force
field (MM2 in Chem3D).
· Use the same keywords
from the example napthalene input file.
· Notice that the
Gaussian program uses keywords to decide what kind of calculation to perform and
what kind of results to produce. The extra keywords, like GFINPUT, IOP(6/7)=3,
and 6D or 5D are required by MOLDEN or JMOL, respectively, to visualize results
from Gaussian.
· Use JMOL and WORD (or
EXCEL) to construct a table showing π molecular orbitals for ethylene
(dienophile) and 1,3-butadiene. In particular, you will be interested in the
HOMO and LUMO for each (you may also want to look at HOMO-1, LUMO+1, and LUMO
+2 if you want to see which reactant orbitals become product orbitals).
· Remember that you
want to select the minimized geometry from the output file for JMOL
to display.
· Use your computed MOs
to verify the reaction mechanism above. Almost any organic text can be
used for additional information.
You can read more about the frontier orbital theory from Kenichi Fukui Nobel Prize lecture.
2. Molecular Surfaces
Molecular Shape Surfaces
The shape of a molecule is determined by the electron density of the molecule and this electron density depends on the atomic composition of the molecule. One way to determine molecular shape is to calculate electron density and display the region where electron density is larger than some cut-off value as a three-dimensional surface. Such calculations necessitate quantum chemical approach and are possible with not too large molecules. For larger molecules, Connolly surfaces and solvent-accessible surfaces can be calculated rapidly based on empirical van der Waals radii of atoms.
Electrostatic Potential Surfaces
 Electrostatic potential surfaces are valuable
in computer-aided drug design because they help in optimization of
electrostatic interactions between the protein and the ligand. These surfaces
can be used to compare different inhibitors with substrates or transition
states of the reaction. Electrostatic potential surfaces can be either
displayed as isocontour surfaces or mapped onto the molecular electron density.
The latter are more widely used because they retain the sense of underlying
chemical structure better than isocontour plots.
Electrostatic potential surfaces are valuable
in computer-aided drug design because they help in optimization of
electrostatic interactions between the protein and the ligand. These surfaces
can be used to compare different inhibitors with substrates or transition
states of the reaction. Electrostatic potential surfaces can be either
displayed as isocontour surfaces or mapped onto the molecular electron density.
The latter are more widely used because they retain the sense of underlying
chemical structure better than isocontour plots.
Example: Oxamic Acid
 This
tutorial illustrates how to use quantum chemistry calculations to generate and
display molecular electron density surfaces and map electrostatic potential values
to the surface. You will compare two conformers of oxamic acid. Oxamate, anion
of oxamic acid is a powerful inhibitor for Plasmodium falciparum
lactate dehydrogenase and thus may serve as a fragment or lead in developing
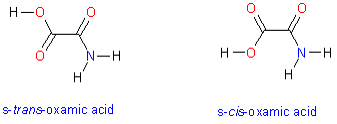
novel anti-malaria drugs. The molecule has two low energy conformers that
differ in the dihedral angle about the central C-C bond. These conformers are
shown in the image on the right.
This
tutorial illustrates how to use quantum chemistry calculations to generate and
display molecular electron density surfaces and map electrostatic potential values
to the surface. You will compare two conformers of oxamic acid. Oxamate, anion
of oxamic acid is a powerful inhibitor for Plasmodium falciparum
lactate dehydrogenase and thus may serve as a fragment or lead in developing
novel anti-malaria drugs. The molecule has two low energy conformers that
differ in the dihedral angle about the central C-C bond. These conformers are
shown in the image on the right.
Your task is to calculate and display electrostatic potential of cis and trans oxamic acid. Molecular surfaces should be calculated based on optimized molecular geometries. While molecular mechanics force fields can be used to generate reasonable initial geometries, it is considered a good practice to optimize molecular geometries with quantum mechanical methods prior to generation of electron molecular electrostatic potential surfaces. In this tutorial you use Chem3D to construct and minimize the cis and trans oxamic acid structures using the MM2 Force Field. The quantum chemistry program Gaussian was used to perform geometry optimization for the two conformers. You will use GRIDCHEM to launch quantum mechanical geometry optimizations but keep in mind that optimizing a larger molecule using accurate QM methods can be very time-consuming. The calculation will be performed at the Moller-Plesset second order perturbation theory level with a moderate-sized basis set to describe molecular orbitals. Specifically, a 6-311+G(d,p) basis set will be used which allows for some polarization of electron density on both heavy atoms and hydrogens. In computational jargon, the molecule will be optimized at the MP2/6-311+G** level. The comparison of relative energies of the two conformers suggests that s-trans conformer is more stable by 1.68 kcal/mol.
· JMOL Properties
Visualization from Gaussian-03 Output File
1.Notice that the
Gaussian program uses keywords to decide what kind of calculation to perform
and what kind of results to produce. The extra keywords, like GFINPUT,
IOP(6/7)=3, and 6D or 5D are required by MOLDEN or JMOL, respectively, to
visualize results from Gaussian. You can modify the Keyword lines to add
advanced options. For example, to request a rather expensive CCSD/cc-pVTZ
calculation, you could change HF/6-31G** to CCSD/cc-pVTZ. Gaussian options are
discussed in detail at http://www.gaussian.com/g_ur/keywords.htm
2.Give an unique and
easy-to-identify name to the job. For example, you may name the trans conforner
oxamic_trans.
3.The title line is for
optional comments. People typically add some description as of the purpose of
this calculation.
4.You can cut and paste
the the xyz-coordinates from Chem3D.
5.Detrmine the
difference in energy between the two conformers.
6.Display the MOs,
especially the HOMO and LUMO, for these conformers using the methods outlined
above.
7.Now let's map the the
molecular electrostatic potential (MEP) onto the solvent_accessible surfaces
for each conformer. Ideally, one would map the MEP onto the molecular
electronic density, however, one needs to calculate a CUBE file from the
Gaussian checkpoint file to complete this task (see below). Open the JMOL
Srcipt console and type: isosurface delete
resolution 6 solvent map mep. Describe what see. What is the
significance ?
8.Play around with some
of the surfaces. Check out this Isosurfaces
Examples page for some ideas..
· JMOL Properties
Visualization from Gaussian-03 CUBE File. The CUBE file are very large,
even compressed. These may take a while to download.
1.Download CUBE files
for trans-oxamic and cis-oxamic acids (you do not need to unzip these files,
JMOL can read the zipped files):
§ trans_den.cube.gz & cis_den.cube.gz
- These files contain the electron density data.
§ trans_pot.cube.gz & cis_pot.cube.gz
- These files contain the electrostatic potential data calculated from
the electron density and nuclear conformation.
§ trans_homo.cube.gz & cis_homo.cube.gz - These files contain
the volumetric data for the HOMO.
§ trans_lumo.cube.gz & cis_lumo.cube.gz - These files contain
the volumetric data for the LUMO.
2. Open JMOL and
the JMOL Srcipt console.
3.Now you must set the
PATH to your working directory in the JMOL Srcipt console. Type: set defaultdirectory
"path-to-working-directory" The quote marks must be used for your
directory.
4.Let's start with the
trans-oxamic acid. Load the coordinates from the density file.
Type: load trans_den.cube.gz - you
should see the molecule in the JMOL dispaly window. You can make it a stick
model by using the pulldown menu DISPLAY:ATOM:NONE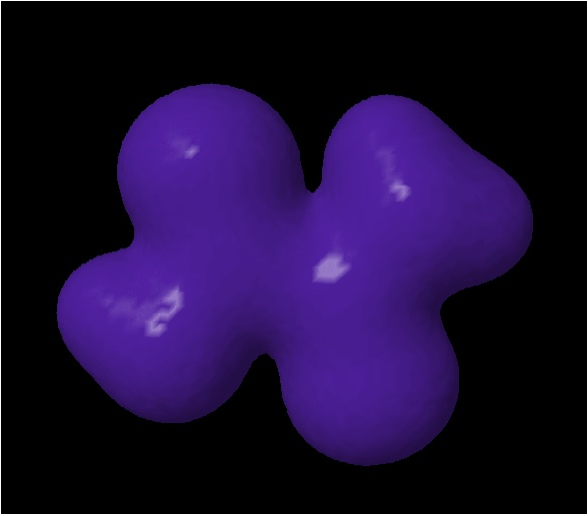
5.Now display the
electron density by typing isosurface
"trans_den.cube.gz" You should see something
like the image to the right.
6.You can change the
value of the isosurface by using the cutoff option: isosurface cutoff 0.01 "trans_den.cube.gz" This just
changes the value of the electron density used to establish the surface.
7.You can also change
the color of the surface; for example: color
isosurface red
8.You can also
make it translucent: isosurface
translucent or a mesh: isosurface nofill
mesh
9.The command isosurface delete will delete the surface.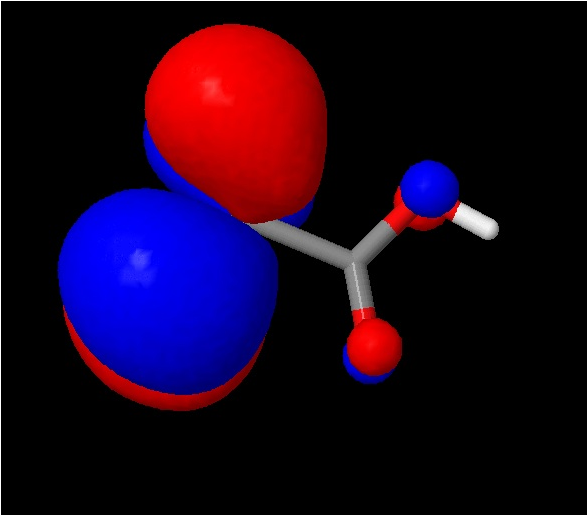
10. Now we will plot a
molecular orbital (the sign option tells Jmol to plot both the positive and
negative lobes): isosurface sign
"trans_homo.cube.gz"
11. 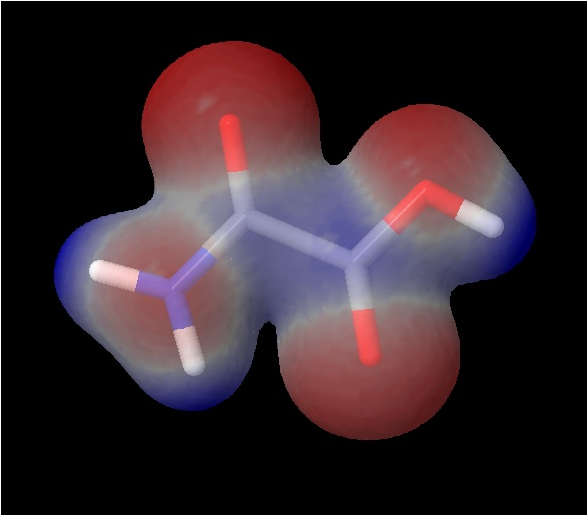 You can also map the
electrostatic potential onto the elctron density isosurface, similary to step
7, above. "isosurface
trans_den.cube.gz" colorscheme
"rwb" color absolute -0.1 0.3 map "trans_pot.cube.gz"
Try not changing the color scheme ("isosurface
trans_den.cube.gz" map
"trans_pot.cube.gz") and see what happens.
You can also map the
electrostatic potential onto the elctron density isosurface, similary to step
7, above. "isosurface
trans_den.cube.gz" colorscheme
"rwb" color absolute -0.1 0.3 map "trans_pot.cube.gz"
Try not changing the color scheme ("isosurface
trans_den.cube.gz" map
"trans_pot.cube.gz") and see what happens.
12. You can also plot
planes through volumetric data rather than plot isosurfaces. Pick three
atom to form a plane (C2 C3 & N4). Then use these three command lines
in sequence:
§ draw myplane (C2) (C3) (N4)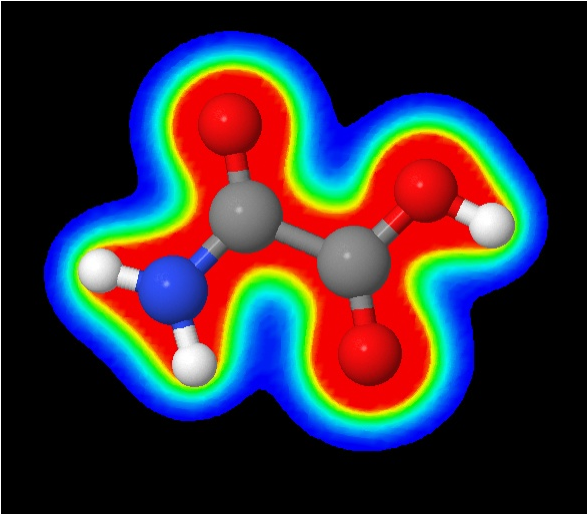
§ draw off
§ isosurface plane $myplane colorscheme "roygb"
color absolute 0.01 0.15 reversecol "trans_den.cube.gz"
13. Repeat for the
cis-oxamic acid and note differences. Play with this - it is very
powerful and instructive.